
-零假設和替代假設(來源:PrepNuggets)
原假設和替代假設(Null and Alternative Hypotheses)
零假設是假設與正常狀態為零或沒有偏差。由於證明假設很困難,我們通常會找到反對原假設的證據並接受替代假設,而不是直接證明替代假設為真。因此,原假設和備擇假設可以寫成如下:
. 替代假設:樣本指紋與模型庫中的模板不匹配
. 零假設:樣本指紋與模型庫中的模板匹配
錯誤接受率 (FAR) 和錯誤拒絕率 (FRR) 等與生物識別相關的術語是常用的,並且對於通信非常有效。人們或書籍將 FAR/FRR 與型一和 型二錯誤(用於統計假設)或假陽性/陰性(用於二元分類)相關聯的情況並不少見。我寫這個問題是為了強調當我們談論 I/II 類錯誤時零假設的重要性。
型一和 型二錯誤(Type I and Type II Errors)
在統計學中,我們通常不會只提出一個需要足夠證據來證明的假設。相反,我們接受備擇假設,因為我們拒絕了基於具有預定義顯著性水平(例如,5%)的反對原假設的證據。
統計假設檢驗的決定是是否拒絕零假設。但是,有些決定可能是錯誤的,可分為以下幾類:
. 第一類錯誤:我們拒絕原假設,這是真的。(拒絕正常情況)
. 第二類錯誤:我們未能拒絕原假設,這是錯誤的。(接受異常情況)
假陽性和假陰性(False Positive and False Negative)
當談到機器學習中的二元分類時,模型被訓練為基於一小部分樣本數據的二元分類器,通過標籤對實例/案例進行分類(例如,0/1、垃圾郵件/非垃圾郵件、武器/無武器) .
在實現基於異常檢測的系統中,它可以使用 Imposter/No Imposter 進行分類,如下所示:
. “冒名頂替者”是正面類的標籤。
. “無冒名頂替者”是負類的標籤。
誤報意味著識別/檢測到冒名頂替者,但決定是錯誤的。假陰性意味著沒有識別/檢測到冒名頂替者,而且該決定是錯誤的。人們通常會將假陽性與 I 類錯誤聯繫起來,將假陰性與 II 類錯誤聯繫起來,即使它們在使用不同技術的上下文中使用。Li 的論文很好地將統計假設檢驗與機器學習二元分類進行了比較。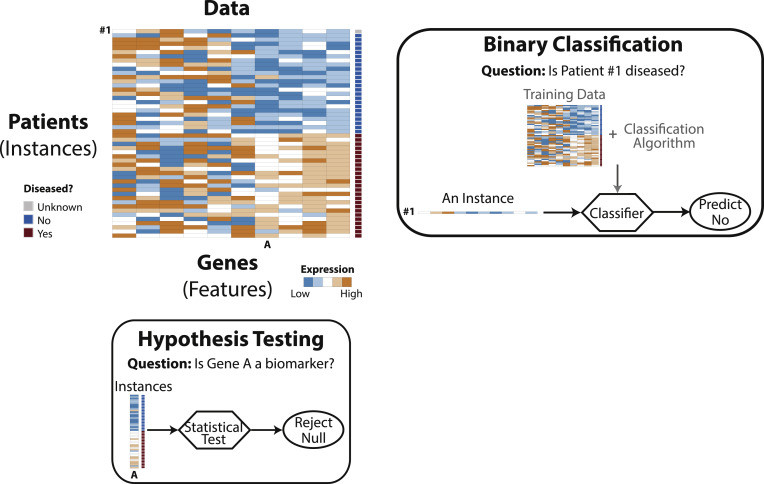
-假設檢驗和二元分類(來源:ScienceDirect)
參考
. 統計假設檢驗與機器學習二元分類:區別和指南
. 統計學中的假設檢驗簡介 – 假設檢驗統計問題和示例
. 假設檢驗簡介
. 機器學習中的 4 種分類任務
. 分類:真與假和正與負
資料來源: Wentz Wu QOTD-20210727
PS:此文章經過作者同意刊登 並且授權可以翻譯成中文
